This post is Part 2 of a series exploring how to value various investment options. Part 1 looked at how to price a US 10 Year Treasury Bond at the time of initial purchase. This post will investigate what happens to the bond price as interest rates rise or fall.
In Part 1, we calculated the current value of the $1000 par value bond paying 3.91% interest biannually over 10 years was $999. You likely noticed that the current value is very close to the $1000 par value of the bond. In fact, it is equal to the par value with the $1 difference due to some rounding error. Why would this be? The calculation of current value is based on the time value of money, meaning that a sum of money is worth more now vs. the same sum of money in the future due to earnings potential in the interim. The earnings potential, called the discount rate, that we apply to value an investment is the current US 10 Year Treasury rate. When valuing the US 10 Year Treasury Bond at the time of purchase, the bonds coupon rate is the current discount rate, so we calculate the current value to be the par value itself.
We saw in 2022 that bond values decreased significantly as the Fed raised interest rates. When the Fed raises interest rates, new issues of US 10 Year Treasury Bonds also increase their coupon interest rate. Existing US 10 Year Treasury Bonds must be repriced using the new discount rate. let's assume that the interest rate is now 5%. What happens to the price of our 3.91% bond we already own? We again break down the valuation into two pieces, first the $1000 par value.
When the bond was issued, in Part 1 we calculated the present value of the par value (principle) as:
PVprincipal = $1,000/(1.0196^20) = $678.94
The new value would be:
PVprincipal = $1,000/(1.025^20) = $610.27
We update the biannual discount rate from 1.96% to the new 2.5%. Intuitively, we know that the price must decrease. No investor would pay the same price for a bond paying 3.91% vs. a bond paying 5%. The 3.91% bond must be discounted.
Remember, we are still receiving the same $19.55 semiannual coupon payments. The 20 coupon payments are also revalued at the 5% discount rate:
PVcoupon = ($19.55/(1.025^1) + ($19.55/(1.025^2) + ($19.55/(1.025^3) + ... ($19.55/(1.025^20) = $303.99
Reminder that the valuation of these coupon payments using the 3.91% discount rate was $320.24.
Summing the two components of the bond we get:
- Old value: $999 (or $1000)
- New Value: $914.26
- Percent change: -8.5%
With little over a 1% increase in interest rates, our bond lost 8.5% in value. The higher the interest rates rise, the less valuable our bond becomes. The converse is also true, if interest rates decrease from the 3.91%, the bond value increases. The following chart shows the principle and coupon payments present value for our bond at different interest rate levels:
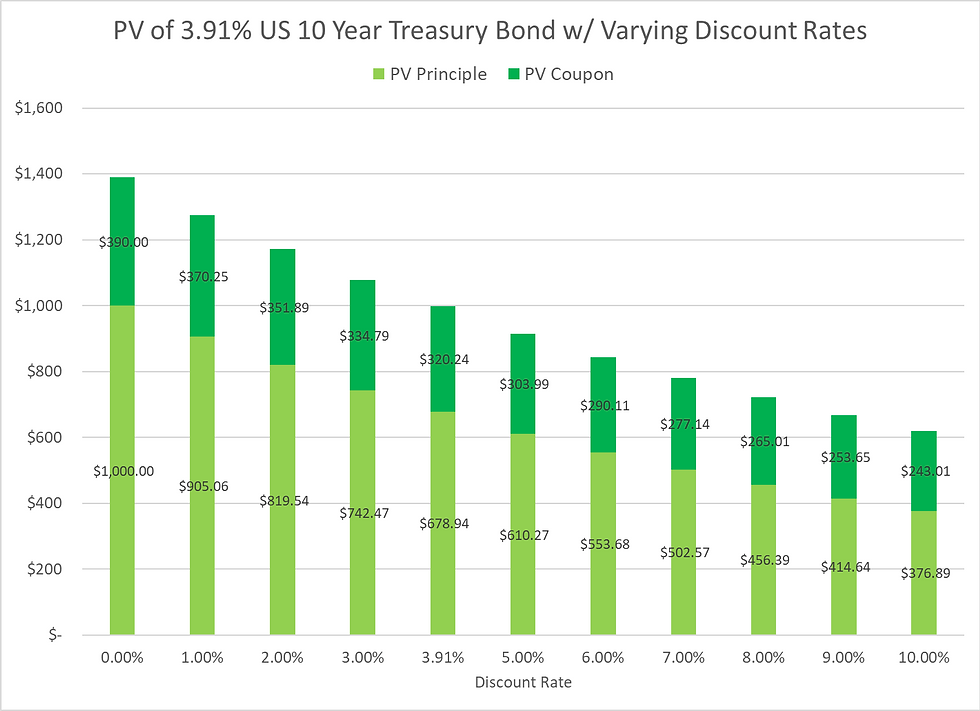
Now we understand why bond funds lost value during 2022 as the Fed quickly raised interest rates. We can also see that at a 0% interest rate, the present value of our bond is simply worth the sum of the coupon payments plus the $1000 par value. Conceptually, at a 0% interest rate there is no longer any return for investing in a risk free US 10 Year Treasury Bond and the time value of money is no longer a factor.
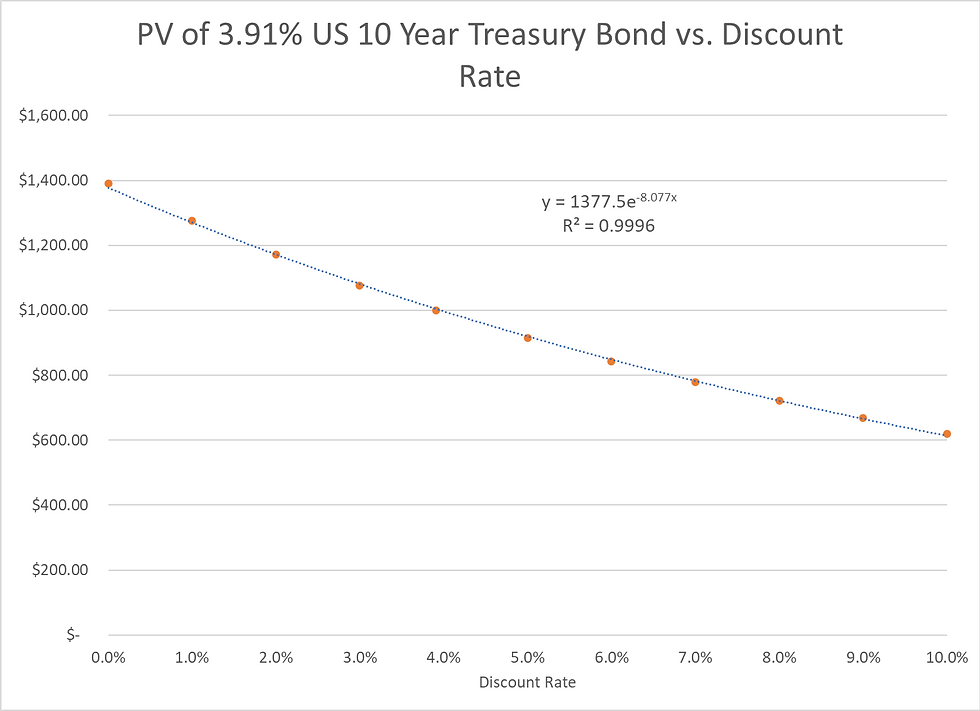
Looking at this same data as a dot plot, we can see that it follows a perfect exponential trend line. The bond value at a 0% interest rate is the sum of the par and coupon payments, while as the interest rates increases, the bond value approached zero (but will never equal zero):
In conclusion, calculating the value of a bond is a straightforward exercise since the future par value and coupon payments are known with 100% accuracy (assuming the US Federal Government does not default). When you invest in bonds, you may hold the bond to maturity or sell it at any point for it's current value. The next post in this series will look at how to value a stock. The concepts are similar to what we have already reviewed, but the inputs are not known with 100% accuracy which presents a more challenging valuation.
Comments