Investment Valuation Part 1 - Bonds
- Josh Pope

- Mar 8, 2023
- 4 min read
Updated: Mar 19, 2023
This post will be part 1 of a series exploring how to value various investment options.
Many investors follow the day to day price changes of stocks, bonds, and other investment assets in their portfolio. Prices bounce around in a chaotic fashion that may appear random and based purely on investor speculation. There is, however, a mathematical process we can use to derive a "true" value of an investment that is simple to understand. This methodology can explain some price movements in the market. For example, why did bond funds suffer large losses in 2022? See this chart of the weekly price in 2022 for the SPDR Portfolio Long Term Treasury ETF:
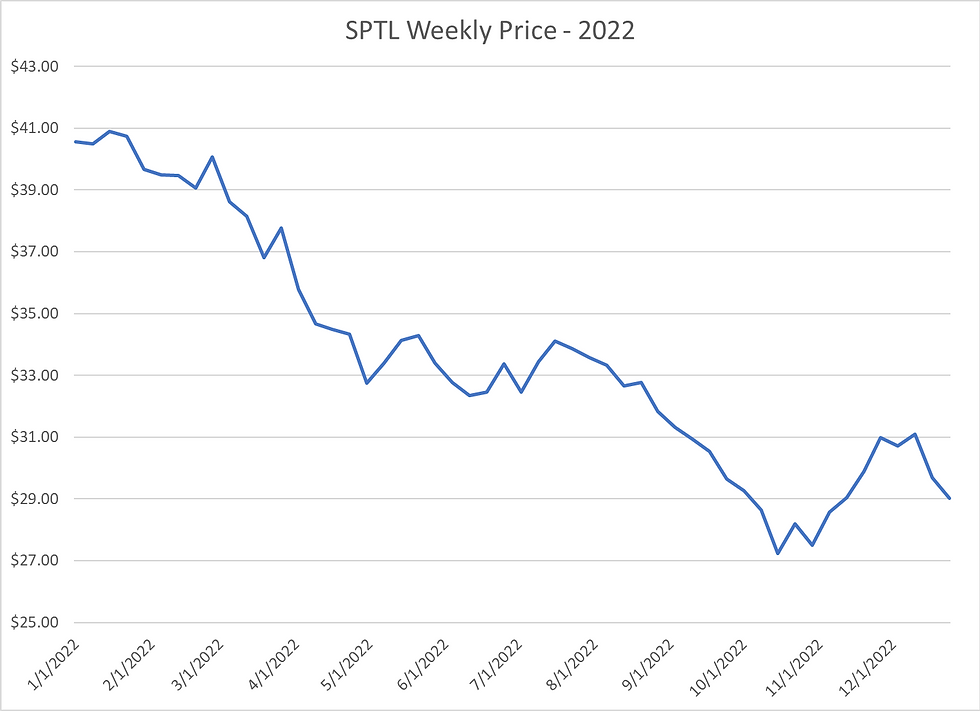
This fund is largely made up of US 10 Year Treasury Bonds. The price fell from $40.57 to $29.03 in 2022, a loss of -28.4%. Some investors include bonds in their portfolios to protect from bear market stock declines. This strategy failed on 2022 as both stocks and bonds fell in tandem. To understand what happened with bond prices, we should look at how bonds can be valued.
A US 10 Year Treasury bond has two components. The first component is a promise to pay the owner the "par" or face value of the bond at expiration, 10 years from the issue date. For our example here, let's use a $1,000 par value bond. If you purchase this bond when issued, 10 years from now the US government will pay you $1,000.
The second component of this bond is the coupon payment. The bond promises to pay you a certain amount of money every 6 months. For a 10 year bond, there will be a total of 20 coupon payments (2 per year). By purchasing this bond you will be paid the 20 coupon payments and then receive $1000 over the 10 year period. This promise is backed by the credit of the US government and is considered "risk free" since the US has never defaulted on a bond promise. The coupon payments are a set $ value but can be described as a interest rate if divided by the par value of the bond. Let's assume our $1,000 bond is from 2/28/2023 when the coupon interest rate was 3.91%. The coupon payment would b $1,000 X (3.91%/2) = $19.55 every 6 months.
In sum, if you bought this bond you would receive the 20 payments of $19.55 and the final $1,000 par value for a total of $1,391. The valuation of this bond answers the question, "What is the value of these payments as of today?" Let's break down the valuation into two parts, first looking at the $1000 par value payment. How much would you pay today to receive $1,000 in 10 years? Obviously, no one would pay $1,000 now to receive $1,000 in 10 years so the current value must be less than $1,000. This is the called the time value of money. The future $1,000 is less valuable because you can invest the $1,000 today and make interest. Also, inflation will likely degrade the future $1,000 purchasing power. To calculate the current value of the future $1,000 payment, we apply a "discount rate". The discount rate commonly used is the current risk free interest rate, for which the 10 Year Treasury rate is used (this is the closest to "risk free" rate we have available). The formula for this calculation is:
PVprincipal = $1,000/(1.0196^20) = $678.94.
Let's break this down. The $1000 is the future par value. The 1.0196 is 1 plus the current 3.91% interest rate divided by 2 to represent the interest rate for each of the biannual periods. The ^20 means to the power of the total number of biannual periods. In other words, if we took $678.94 today and received 20 compounded interest payments of 1.96% each, we would end up with $1,000 in 10 years. The table below applies this same calculation and shows the current value for each 6 month period from purchase:
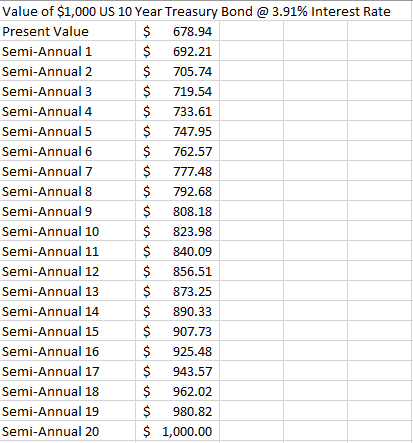
The par value portion of the bond increases in value as we approach the 10 year term. This is intuitive since an investor would pay more for a guaranteed $1,000 in 5 years vs. receiving the same payment in 10 years.
Now that the par value portion of the bond is valued, we can look at the other part of the bond, the coupon payment. The same time value of money principle applies as we simply have to discount the coupon payments using the same formula as the par value. The difference here is that rather than a single $1,000 payment in 10 years, we have 20 payments of $19.55 occurring every 6 months. Each payment is discounted separately and summed as follows:
PVcoupon = ($19.55/(1.0196^1) + ($19.55/(1.0196^2) + ($19.55/(1.0196^3) + ... ($19.55/(1.0196^20)
The following table shows the present value of each coupon payment and the overall sum:
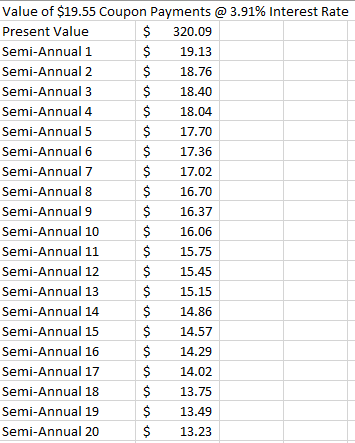
As expected, the further into the future the payment, the less it is worth today. The sum of the present value of each payment is $320.09.
We add this to the present value of the par value to get the total present value of this bond: $678.94 + $320.09 = $999.
The value of a bond fluctuates based on the prevailing risk free interest rate. In the next post we will see what happens to bond value when the interest rates increase or decrease and explain the bond price performance in 2022.






Comments